炼丹实战(2):第一炉丹

发表于 | 更新于: | 分类于
字数统计: 2.4k | 阅读时长 ≈ 10

前言

上一篇了解了丹炉后，那么这一次，我们就要动手实践，炼制自己的第一炉丹药了。万事皆应由易向难，说到最简单的丹药，那自然是一品丹药「回春散」了。咳咳~ 那么这一篇就从简单的回归讲起，主要是让大家熟悉一下，TensorFlow 的处世哲学，看看 TensorFlow 是怎么解决问题的。

粗糙的·回春散

最简单的回归问题当属线性回归了，线性回归的问题估计每位同学都在初中就有所接触。我还记得，当时我们老师不允许我们用计算器，用「最小二乘法」算一次线性回归的问题，那起码是十来分钟啊。当然，这还不包括有时粗心算错数值，三次得出三个不一样的结果了。

「最小二乘法」用于解决线性拟合的问题，可以以最小的损失找到一条拟合散点的直线。而且也有现成的公式，一个循环，或者矩阵相乘就能解决。但是 TensorFlow 处理问题的逻辑不是这样的，那么就来看看 TensorFlow 是怎么解决问题的吧！

我们使用更加简单的问题，就是没有误差的一条直线，让 TensorFlow 来解决。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import tensorflow as tf
import numpy as np

x_data = np.random.rand(10)
y_data = x_data * 0.1 + 0.2

b = tf.Variable(0.)
k = tf.Variable(0.)
y = k * x_data + b

loss = tf.reduce_mean(tf.square(y_data - y))
train = tf.train.GradientDescentOptimizer(0.2).minimize(loss)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer()) # Variable(变量)使用前需要初始化
    for step in range(401):
        sess.run(train)
        if step % 20 == 0:
            print step, sess.run([k, b])

这里的数据是随机生成的 10 组，但每一个点准确的落在 $ y = kx+b $ 这条直线上。

注意看 sess 这个员工每一次干了什么事：首先他要运行 train 这个 op，而 train 这个 op 的任务是「使用梯度下降法，让 loss 变得最小」，继续追溯， $ loss = \frac{\sum{(y_{data} - y)^2}}{n} $ ， $ y = k·x_{data} + b $ ，那么整个的任务中，就只有 k 和 b 是可以调整的变量。因此，sess 这个员工就会依照「梯度下降法」的原则，不断的调整 k 和 b。

TensorFlow 的这种处理问题的逻辑和平时的公式或者特定的算法不一样，简单的说，就是 不断的调整可变量，使得误差最小 。这种逻辑在处理线性回归这种简单的问题上时显得繁琐了一些，但是若是处理更加复杂的问题，就会简单得多。因为，复杂的问题，还是一样地缩小误差，不是吗？

上面的代码让每训练20次输出一次结果，那么一起来看看结果吧：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
0 [0.037390854, 0.09433242]
20 [0.09015258, 0.20382951]
40 [0.094809845, 0.20201874]
60 [0.09726442, 0.20106402]
80 [0.09855816, 0.20056081]
100 [0.09924004, 0.20029558]
120 [0.09959945, 0.2001558]
140 [0.09978888, 0.20008212]
160 [0.09988872, 0.20004328]
180 [0.09994134, 0.20002282]
200 [0.099969074, 0.20001203]
220 [0.09998371, 0.20000634]
240 [0.099991426, 0.20000334]
260 [0.09999547, 0.20000176]
280 [0.09999761, 0.20000094]
300 [0.09999873, 0.20000051]
320 [0.09999934, 0.20000026]
340 [0.09999966, 0.20000014]
360 [0.09999981, 0.20000008]
380 [0.09999985, 0.20000006]
400 [0.09999985, 0.20000006]

可以看到，k 从一开始的 0.037 逐渐调整为 0.099，b 从一开始的 0.094 调整为 0.200。最忽略误差的情况下，我们可以认为程序已经找到了 k = 0.1, b = 0.2 的这个正确结果。

普通的·回春散

那么这一次，我们来给数据掺杂，使得数据在 $ y = kx+b $ 的附近波动。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

x_data = np.linspace(-0.5, 0.5, 20)
noise = np.random.normal(0, 0.01, x_data.shape)
y_data = 0.1 * x_data + 0.2 + noise

b = tf.Variable(0.)
k = tf.Variable(0.)
y = k * x_data + b

loss = tf.reduce_mean(tf.square(y_data - y))
train = tf.train.GradientDescentOptimizer(0.2).minimize(loss)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for step in range(401):
        sess.run(train)
        if step % 20 == 0:
            print step, sess.run([k, b])
    prediction = sess.run(y)

plt.figure()
plt.scatter(x_data, y_data)
plt.plot(x_data, prediction, 'r-', lw=5)
plt.show()

还是一样的逻辑，下面是运行结果：

运行结果

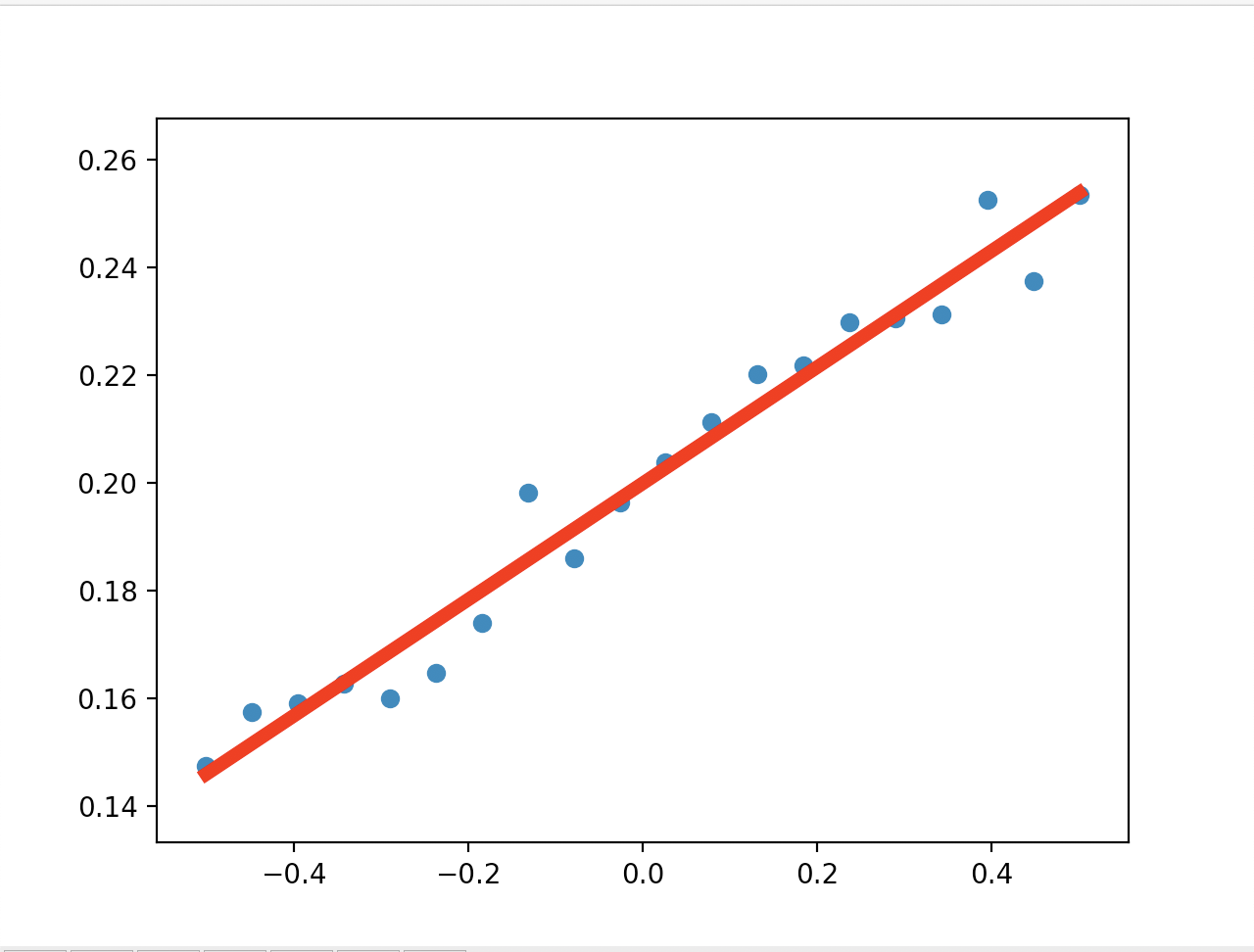
还有训练的数据：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
0 [0.0039783507, 0.07995532]
20 [0.05889236, 0.19988391]
40 [0.08481223, 0.19988827]
60 [0.097046636, 0.19988827]
80 [0.10282137, 0.19988827]
100 [0.1055471, 0.19988827]
120 [0.10683367, 0.19988827]
140 [0.107440926, 0.19988827]
160 [0.107727565, 0.19988827]
180 [0.10786287, 0.19988827]
200 [0.107926734, 0.19988827]
220 [0.10795687, 0.19988827]
240 [0.107971095, 0.19988827]
260 [0.107977815, 0.19988827]
280 [0.107981, 0.19988827]
300 [0.107982494, 0.19988827]
320 [0.10798319, 0.19988827]
340 [0.10798353, 0.19988827]
360 [0.10798368, 0.19988827]
380 [0.10798372, 0.19988827]
400 [0.10798372, 0.19988827]

可以看到，即使数据有所波动，程序还是准确的将 k 和 b 调整到了 0.1 和 0.2 的附近。

PS：要注意的是，TensorFlow 的数据的值也要在 Session 中使用 run() 来获取哦！

优秀的·回春散

线性回归的问题解决了，那么来试试非线性的吧！

这里就直接用掺杂的数据了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

x_data = np.linspace(-0.5, 0.5, 200)[:, np.newaxis]
noise = np.random.normal(0, 0.02, x_data.shape)
y_data = np.square(x_data) + noise

x = tf.placeholder(tf.float32, [None, 1])
y = tf.placeholder(tf.float32, [None, 1])

a = tf.Variable(0.)
b = tf.Variable(0.)
c = tf.Variable(0.)
y_pre = a * tf.square(x) + b * x + c

loss = tf.reduce_mean(tf.square(y - y_pre))
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(2000):
        sess.run(train_step, feed_dict={x: x_data, y: y_data})

    prediction_value = sess.run(y_pre, feed_dict={x: x_data})
    print 'result: ', sess.run([a, b, c])

plt.figure()
plt.scatter(x_data, y_data)
plt.plot(x_data, prediction_value, 'r-', lw=5)
plt.show()

这里的 x 和 y 的数据都是在使用的时候传进去的，而不是像前面一样一开始就定死的。placeholder 和 feed 具体的用法可以自行搜索，

下面是拟合的结果：

拟合结果

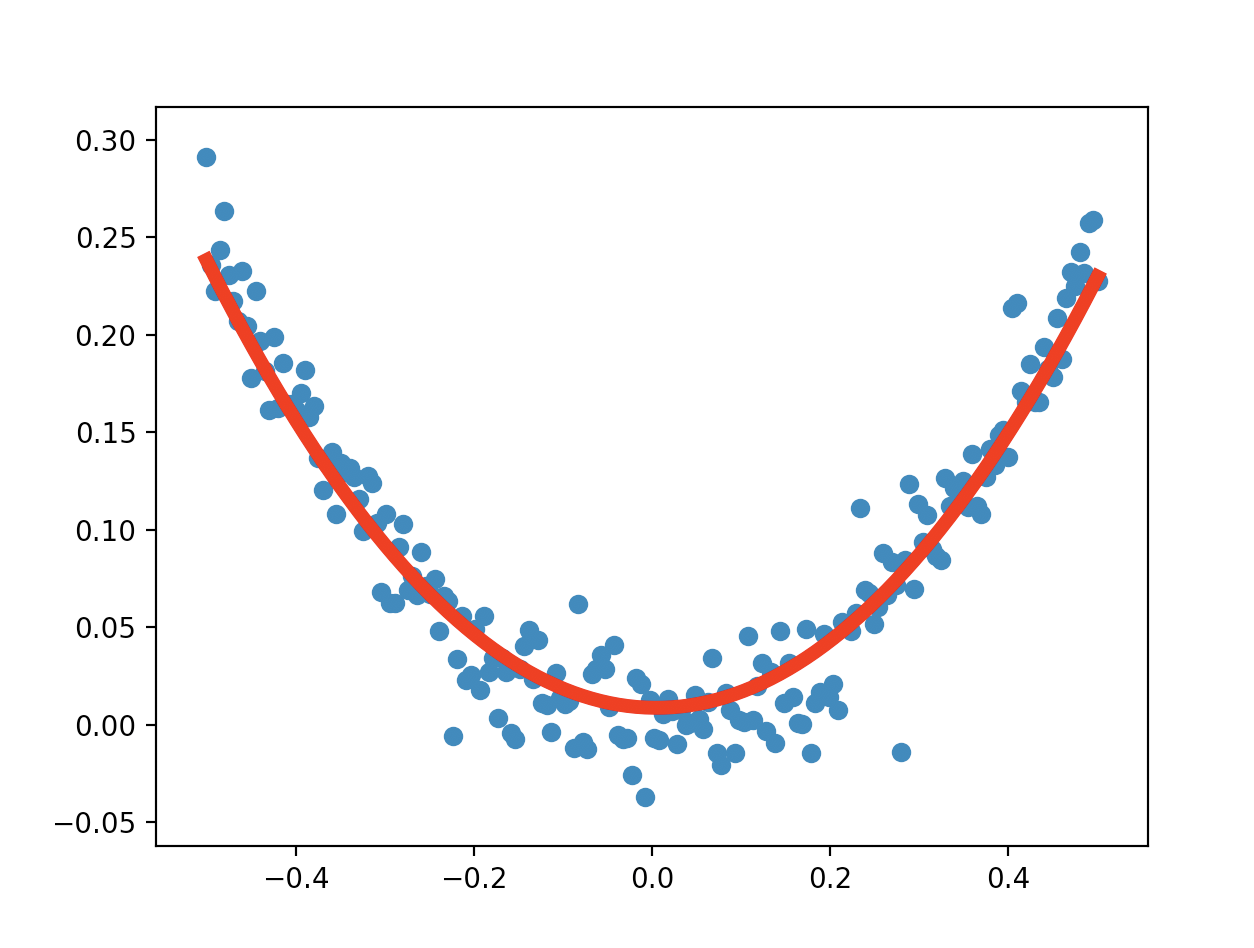
输出的参数 a, b, c：

1
result:  [0.9012379, -0.008498974, 0.008641074]

精良的·回春散

对深度学习和神经网络有一些了解的小伙伴应该可以看出来，上面的三个都是只有输入和输出层，没有中间层的。而且，上面的程序都是我们确定好了回归的类型，即我们知道结果应该是线性，或者二次函数，然后我们去拟合它，寻找最佳的参数。既然要用 TensorFlow，那么自然也要加一层中间层才像样子嘛~

前面的模型都是：

【输入层】 =====( * 权重 + 偏置值) =====> 【输出层】

加了中间层之后：

【输入层】 =====( * 权重 + 偏置值) =====> 【中间层】 =====( * 权重 + 偏置值) =====> 【输出层】

中间层的节点可以不止一个，因此，两级的权重和偏置值都是矩阵的形式。不同于前面的，我们不需要知道我们拟合的是什么类型的函数，我们只需要中间的两层权重和偏置值矩阵就行了；我们也不需要知道这两层的值是怎么调整出来的，因为 TensorFlow 会自动为我们调整；我们更不需要知道为什么这样可以，只要准确率达到我们的期望就可以。我们需要做的，只是将图的结构画出来，Session 会直接根据变量之间的关系进行调整。

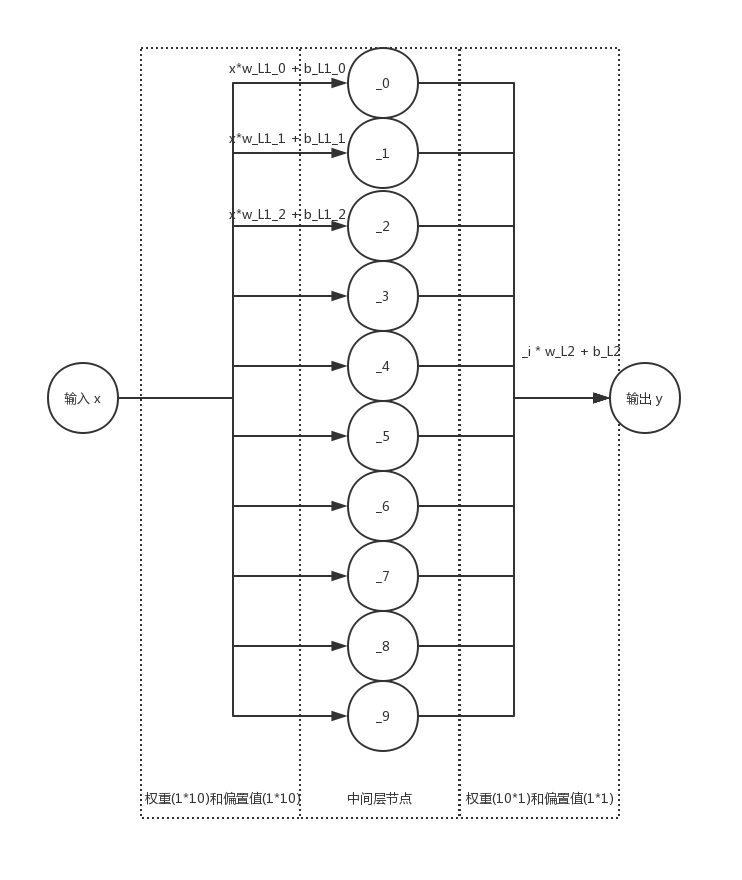
网络的结构

如上图所示，输入的 x 与 1 行 10 列的权重矩阵相乘，得出一个 1 行 10 列的矩阵，再加上同样是 1 行 10 列的偏置值，成为中间节点的值。中间节点值为 1 行 10 列的矩阵，与第二层 10 行 1 列的权重矩阵做矩阵乘法，得出一个 1 行 1 列的数值，加上第二层的偏置值，结果就是输出 y。我们说需要的就是两层的权重和偏置值，但是为什么这样，原理是什么，为什么它这样可以拟合，我们完全不需要知道。

注意： 上图没有画激励函数的部分，乘上权重加上偏置值之后需要放入激励函数中，以引入非线性因素（如果不加入的话，y 和 x 依然是「线性关系」），更多关于激励函数的内容可以自行上网搜索。

接下来就是代码的部分了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

x_data = np.linspace(-0.5, 0.5, 200)[:, np.newaxis]
noise = np.random.normal(0, 0.02, x_data.shape)
y_data = np.square(x_data) + noise

x = tf.placeholder(tf.float32, [None, 1])
y = tf.placeholder(tf.float32, [None, 1])

Weight_L1 = tf.Variable(tf.random_normal([1, 10]))
biases_L1 = tf.Variable(tf.zeros([1, 10]))
Wx_plus_b_L1 = tf.matmul(x, Weight_L1) + biases_L1
L1 = tf.nn.tanh(Wx_plus_b_L1)

Weight_L2 = tf.Variable(tf.random_normal([10, 1]))
biases_L2 = tf.Variable(tf.zeros([1, 1]))
Wx_plus_b_L2 = tf.matmul(L1, Weight_L2) + biases_L2
prediction = tf.nn.tanh(Wx_plus_b_L2)

loss = tf.reduce_mean(tf.square(y - prediction))
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(2000):
        sess.run(train_step, feed_dict={x: x_data, y: y_data})
    prediction_value = sess.run(prediction, feed_dict={x: x_data})

plt.figure()
plt.scatter(x_data, y_data)
plt.plot(x_data, prediction_value, 'r-', lw=5)
plt.show()
  • 使用 tanh 作为激励函数
  • 使用梯度下降法训练
  • 损失为差平方的均值
  • 注意观察两层的网络结构以及数据之间的流动关系

运行的结果：

拟合结果

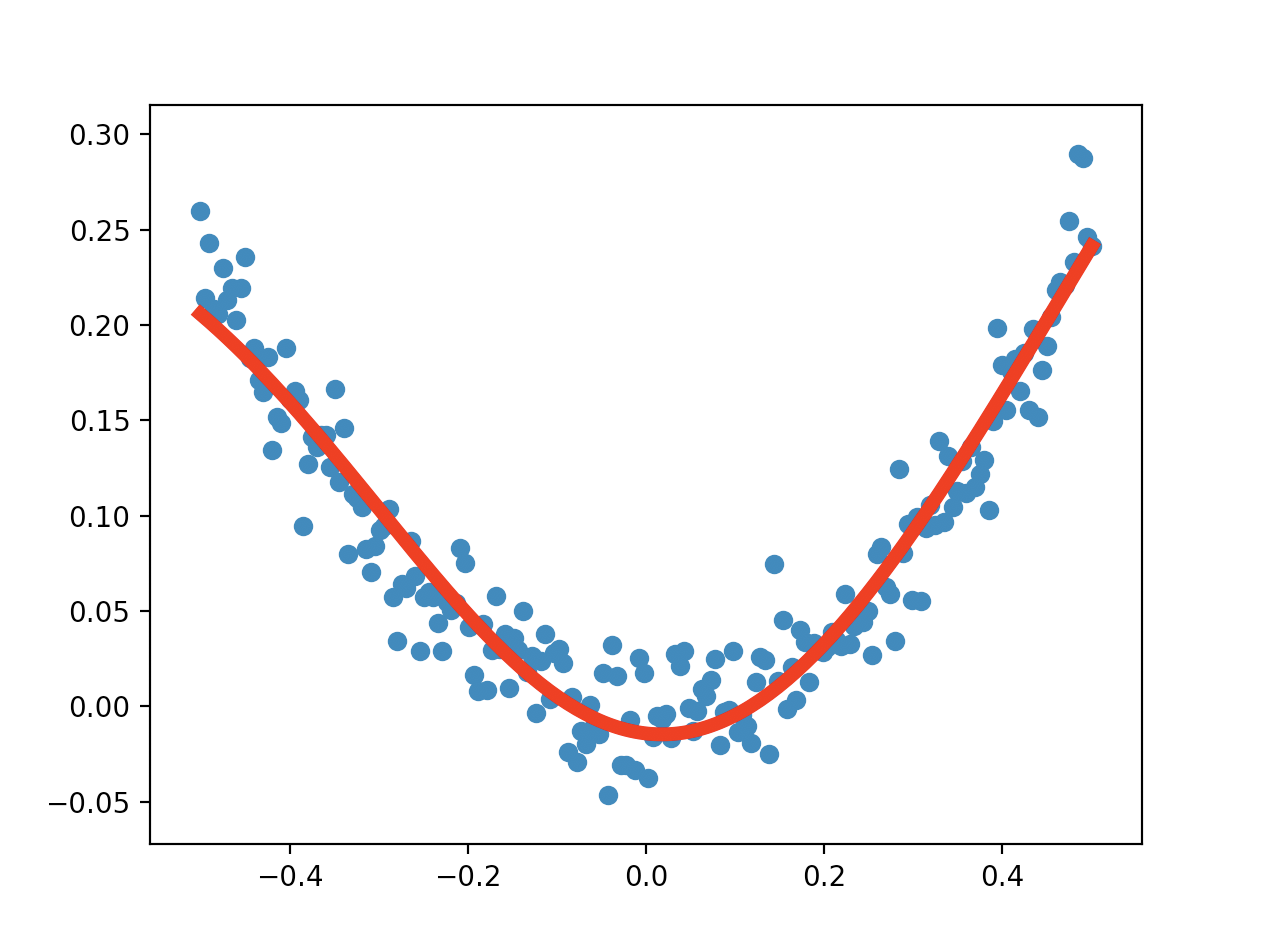
注意观察曲线的两端，可以明显的看到和之前二次函数直接拟合的区别。

后记

上文 4 段代码解决了一些简单的回归问题，通过这些问题的解决，我们可以看出 TensorFlow 简单但又十分高效的处理问题的逻辑。在今后的漫漫炼丹路上，可能会遇到更多复杂的问题，但自动化的炼丹让我们可以将更多的精力投入到丹方的研究上。

要学习的内容还有很多，加油吧~~

0%